線形回帰モデルのL1正則化

事前分布に独立なラプラス分布を仮定してMAP推定を行なうと、L1正則化の効果が出現する。

ラプラス事前分布

独立な正規分布を事前分布とするMAP推定にはL2正則化の効果がある。これは正規分布の指数関数内にL2ノルムが含まれることに由来する。

\begin{aligned} p(\bm w) = \mathcal{N}_d (\bm w | \bm 0, \tau^2 \bm I_d) \propto \exp \left(-\frac{1}{2s^2} \| \bm w \|_2^2 \right) \end{aligned}

そこで、代わりに次のような指数関数内にL1ノルムが含まれる分布を仮定する。これは ラプラス分布 (Laplace distribution) と呼ばれる分布である。

\begin{aligned} \mathcal{La} (w_j | 0, b) \propto \exp \left(-\frac{1}{b} |w_j| \right) \end{aligned}

多変量分布に拡張すると次のようになる。

\begin{aligned} p(\bm w) = \mathcal{La}_n (\bm w | \bm 0, b \bm I_n) = \exp \left(-\frac{1}{b} \| \bm w \|_1 \right) \end{aligned}

このとき、事後分布は次の関数に正規化定数が掛けられた形になる。

\begin{aligned} p(\bm w | \bm X, \bm y) \propto{}& \mathcal N_d(\bm y | \bm X \bm w, \sigma^2 \bm I_n) \mathcal{La}_n(\bm w | \bm 0, b \bm I_n) \\ \propto{}& \exp \left( -\frac{1}{2\sigma^2} \| \bm y - \bm X \bm w \|_2^2 \right) \exp \left( -\frac{1}{b} \| \bm w \|_1 \right) \\ \propto{}& \exp \left( -\frac{1}{2\sigma^2} \left( \| \bm y - \bm X \bm w \|_2^2 + 2\lambda \| \bm w \|_1 \right) \right) \end{aligned}

ただし $\lambda \coloneqq \dfrac{\sigma^2}{b}$ である。

LASSO

MAP推定量は次式のようになる。

\begin{aligned} \hat{\bm w} &= \argmax_{\bm w} \log p(\bm w | \bm X, \bm y) \\ &= \argmin_{\bm w} \left( \|\bm y - \bm X \bm w\|_2^2 + 2 \lambda \| \bm w \|_1 \right) \end{aligned}

これは次のようなL1ノルム罰金項を含む最適化問題の解である。

\begin{aligned} &\underset{\bm w}{\text{minimize}} && \sum_{i=1}^d \left( y_i - \bm w^\mathsf{T} \bm x_i \right) + 2 \lambda \| \bm w \|_1 \end{aligned}

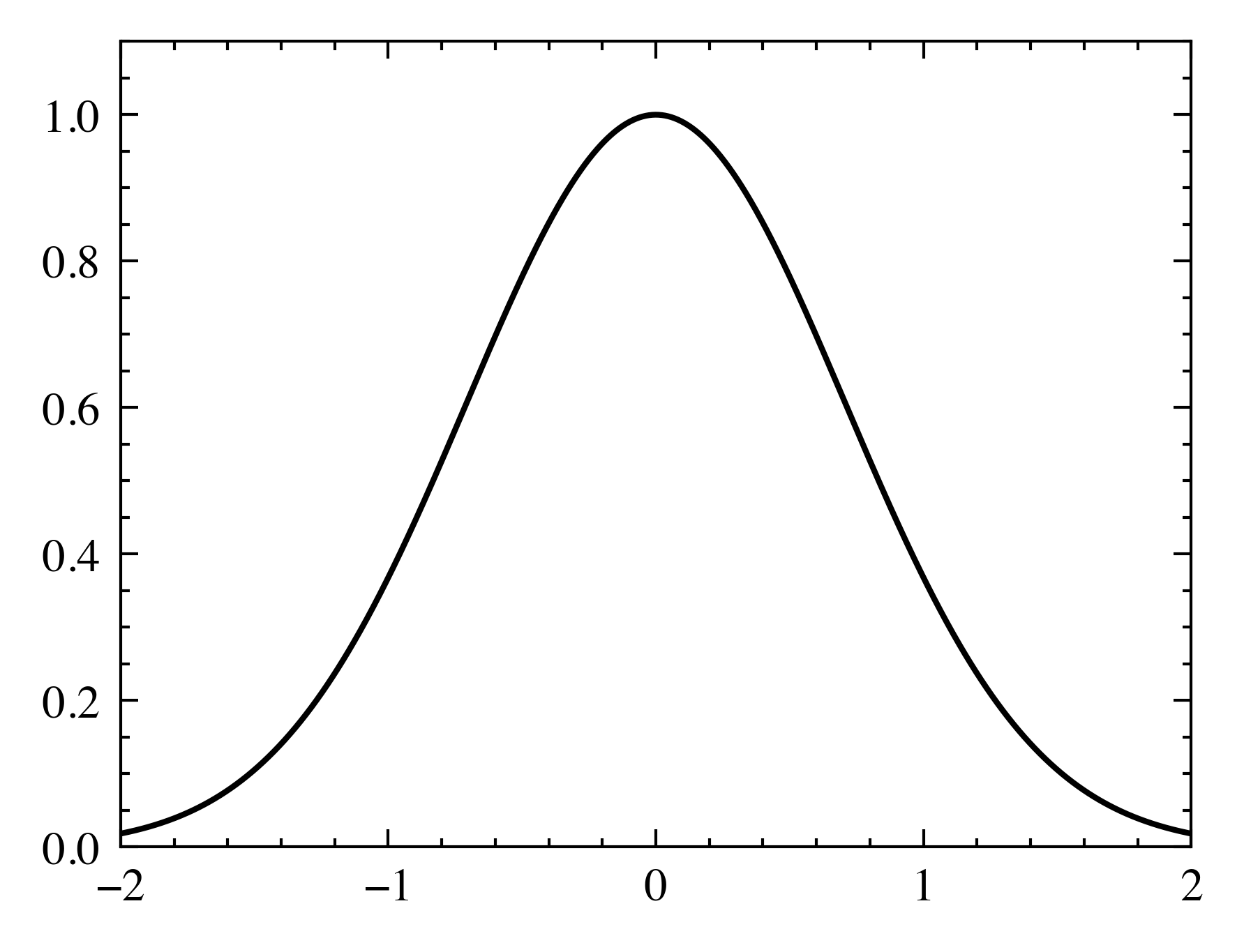
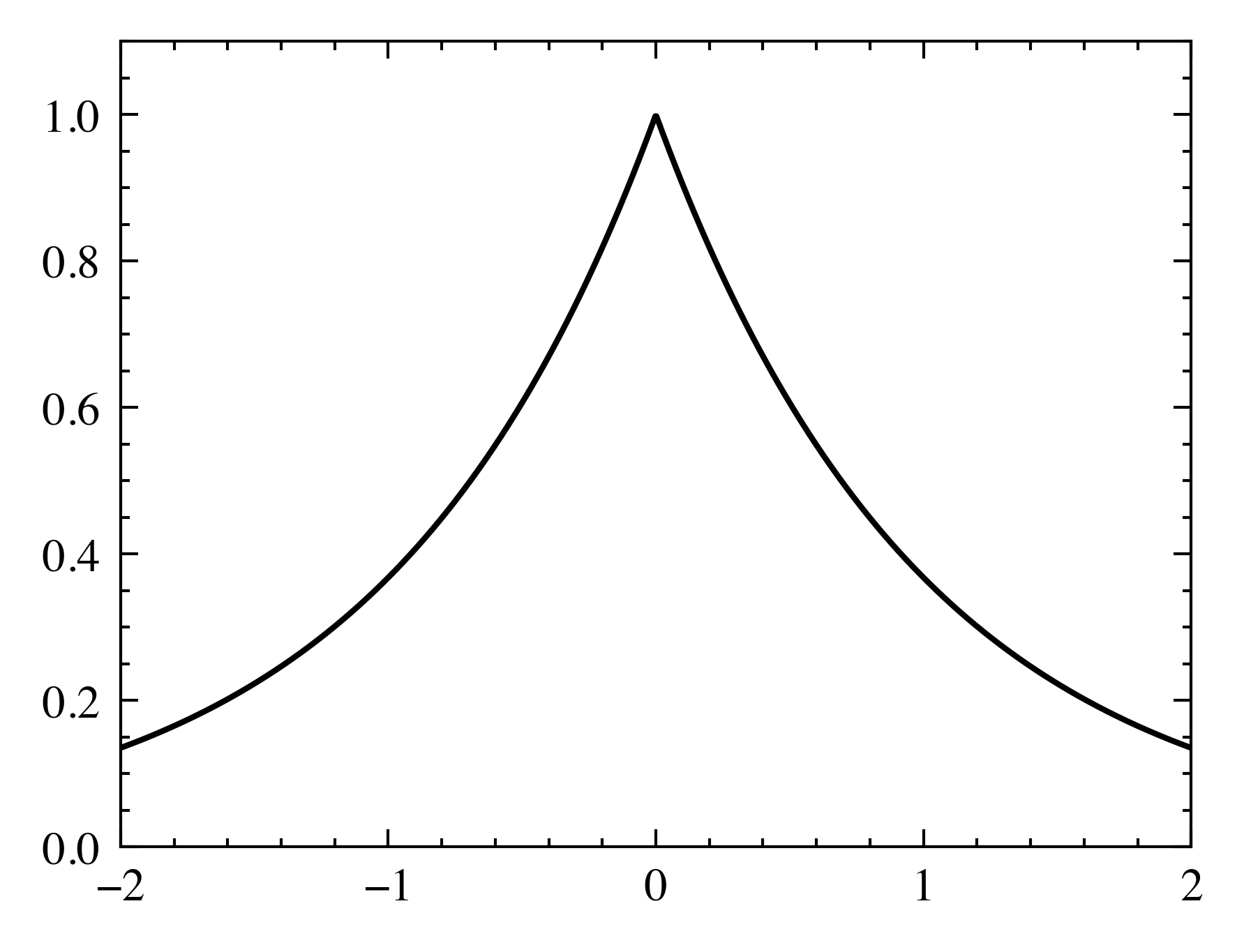
ラプラス分布は図2のようにゼロにおいて尖った形をしている。これはパラメータがゼロとなりやすいことを示唆しており、実際、L1ノルム罰金項を追加してパラメータを推定すると、ゼロとなる値が増えやすいことが知られている。このことから、L1ノルム罰金項を含む推定方法はしばしばLASSO (least absolute shrinkage and selection operator; 最小絶対縮小・選択作用素) と呼ばれる。LASSOを用いた回帰は俗にLASSO回帰などと呼ばれる。

L1正則化

目的関数にL2ノルム罰金項を追加することをL2正則化ということを模して、L1ノルム罰金項を追加することを俗にL1正則化 (L1 regularization) という。当然ながら「正則化」のもとの意味である「正則行列化」という意味は失われている。

\begin{aligned} &\underset{\bm w}{\text{minimize}} && \sum_{i=1}^d \left( y_i - \bm w^\mathsf{T} \bm x_i \right) + \lambda \sum_{j=1}^n |w_j| \end{aligned}

なお、最小二乗法やRidge回帰は解析的にパラメータを計算することができたのに対し、L1ノルム罰金項を含む場合は目的関数に絶対値が含まれるためかなり難しい。